Blog

В ME.BECS можно очень легко и без гемора работать с данными многопоточно.

Давайте разберем как это выглядит на примере простой системы:

- У нас есть сущности с компонентом:

struct ReloadableComponent {
  public float reloadTimer; // время текущей перезарядки
  public float reloadTime;  // сколько идет перезарядка
}

- Нам нужно выбрать все сущности, на которых нет ReloadedComponent

- Для каждой сущности нужно покрутить таймер перезарядки

- Если перезарядка завершена - добавить компонент ReloadedComponent

Итак, приступим.

Сначала создадим систему:

struct ReloadSystem : IUpdate {
  public void OnUpdate(ref SystemContext context) {
     
  }
}

Теперь в метод OnUpdate добавим фильтр по нашему компоненту и каркас для джобы:

struct ReloadSystem : IUpdate {
  
  [BurstCompile] 
  public struct Job : IJobParallelForComponents<ReloadableComponent> {
      public float dt;
      public void Execute(in Ent ent, ref ReloadedComponent component) {
         // тут напишем саму джобу
      }
  } 

  public void OnUpdate(ref SystemContext context) {
     var dependsOn = API.Query(in context)
                        .Without<ReloadedComponent>()
                        .With<ReloadableComponent>()
                        .ScheduleParallelFor<Job, ReloadableComponent>(new Job() {
                          dt = context.deltaTime, 
                        });
     context.SetDependency(dependsOn);
  }
}

А теперь добавим саму логику джобы:

  public struct Job : IJobParallelForComponents<ReloadableComponent> {
    public float dt;
    public void Execute(in Ent ent, ref ReloadedComponent component) {
        component.reloadTimer += this.dt;
        if (component.reloadTimer >= component.reloadTime) {
           ent.Set(new ReloadedComponent());
        }
    }
  } 

Ну собственно и все :)

Теперь это работает многопоточно, под берстом и может быть использовано в общем графе систем.

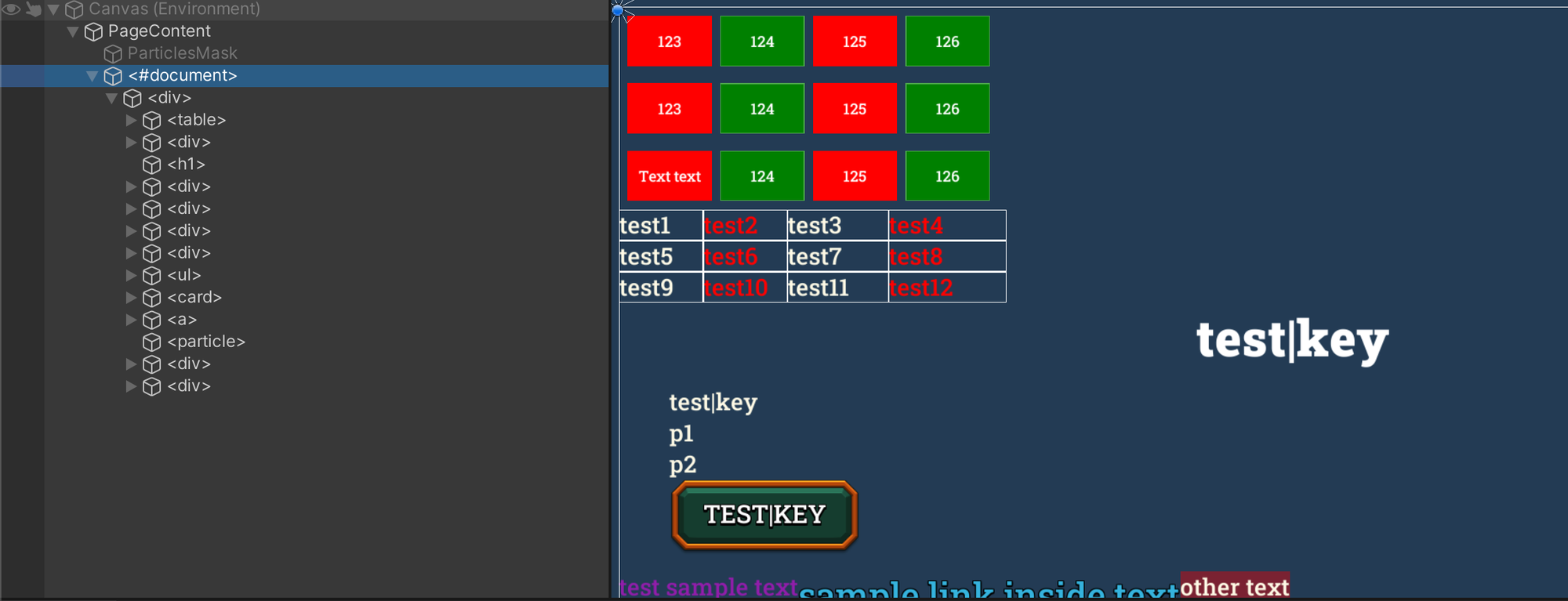
Итак, для ME.BECS (https://github.com/chromealex/ME.BECS) я начал писать поиск пути, ну вот который из коробки там будет.

Для этого я поставил несколько условий:

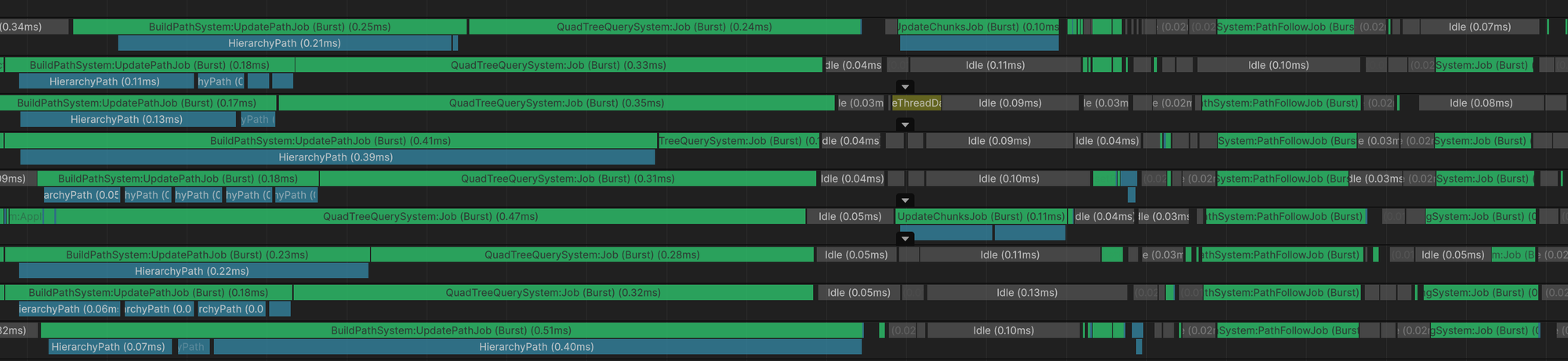
1. Все максимально должно быть burst + многопоточно (ну собственно как и ME.BECS)

2. От количества юнитов производительность зависит минимально

3. Много динамических препятствий

4. Юниты могут толкаться и обходить друг друга без необходимости перестраивать путь

5. Мир может быть довольно большим

Введение

Те, кто читают мой канал https://t.me/unsafecsharp, знают, что для реализации задуманного подходит алгоритм Flow Field.

На самом деле с ним все хорошо, кроме того, что его стоимость W * H, то есть если у нас карта 100х100, то нужно будет обойти 10000 нод. А если 500х500, то уже 250000. Несомненный плюс в том, что перестраивать путь не нужно и количество юнитов ограничено лишь производительностью их алгоритма перемещения.

Общая идея заключается в том, чтобы объединить два подхода: A* и FlowField. 

Для начала разделим все пространство на чанки (размер каждого чанка возьмем, например, 20х20).

Между чанками найдем все пересекающиеся ноды, т.е. те ноды, которые проходимые и их соседи принадлежат другому чанку. Таким образом, получаем некие переходы между чанками, будем называть их порталами (а локальными порталами - порталы, принадлежащие одному чанку).

Первый этап - обновление графа

На самом деле вы можете подумать, а почему обновление, а где построение? И это правильный вопрос, но ответ на него в пункте 3 (много динамических препятствий). По сути если мы сделаем полностью динамический мир - стоимость должна быть такой же как и со статическим.

Итак, вернемся :)

Необходимо построить путь от каждого локального портала во все другие локальные порталы. Для этого будем использовать алгоритм А* или dijkstra (в этом случае не принципиально). Если путь найден - значит из портала можно выйти в другой портал. Если порталы соединяются в одну цепочку - этой цепочке присваивается уникальный айдишник Area (оно пригодится чуть позже).

Стоимость этого перехода будет равна длине найденого пути. Эту операцию можно отнести к разряду редких, т.к. выполняться должна только в случае изменения чанка (например, в чанке появляется или исчезает препятствие).

Мы получим 2 графа: верхнего уровня и нижнего. 

Граф верхнего уровня - это граф (у пустого поля каждый чанк имеет 4 ноды), соединяющий чанки. 

Граф нижнего уровня - это сами чанки, а каждый чанк - это по сути отдельный граф 20х20 нод.

Пустой чанк

Чанк с препятствием

Обновлять чанки мы будем только те, которые изменяются, когда в них добавляется объект, меняющий свойства нод.

Второй этап - обновление пути

Вы спросите, а почему... Ну камон, мы это уже проходили :)

Теперь мы готовы строить (пардон, обновлять) наш путь. В отличие от Flow Field (где не важна точка старта), нам все же нужны точки старта. Но нам нужно собрать информацию обо всех стартовых точках и для каждой начальной точки получить чанк. И вот список уникальных чанков - это и есть наши точки старта.

Т.е. если у нас 1000 юнитов находятся в одном чанке, то поиск пути сработает для всех один раз. Если они занимают разные чанки, будем искать от каждого. Значит стоимость будет O(n).

Этап первый - найти путь на верхнем графе, это будет довольно быстро, т.к. нод в верхнем графе совсем немного. Путь ищем от каждого чанка до конечного чанка.

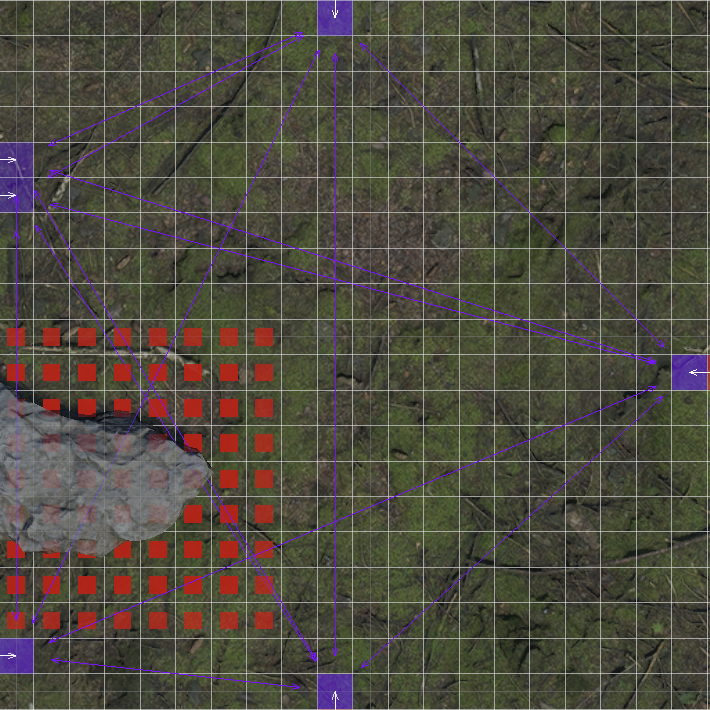
Этап второй - обработать каждый чанк и построить Flow Field. По сути тут типичное построение: начиная с конечной точки (мы выдаем ей стоимость 0) начинаем расходиться в 4 стороны и увеличивать стоимость на размер ноды, при этом стоимость непроходимых нод максимальная, а промежуточные значения - это зоны меньшей проходимости. В итоге получим поле со стоимостями. В этом же проходе мы можем рассчитать LoS (Line of Sight - прямой обзор до конечной точки). Следующим шагом нужно рассчитать направление: берем каждую ноду и считаем минимальную стоимость проходя 8 соседей. Где минимальная стоимость - туда и смотрим. Таким образом мы получаем Flow Field, но он получается строго направленный.

Чтобы сгладить направления, я придумал увеличивать стоимость не на размер ноды, а на дистанцию до цели. Таким образом ноды, которые находятся не на линии конечной точки будут иметь расходящиеся веса. А при вычислении направления мы учитываем веса соседних нод, чтобы определить куда повернуть направление.

Так выглядит Flow Field

Поддержка юнитов разных размеров

На самом деле тут все стандартно: строим не один граф, а несколько графов, накладываем друг на друга, а вокруг препятствий увеличиваем радиус агента.

Высоты

Я добавил для каждой ноды не только стоимость, но и высоту, тем самым получил возможность двигать агентов, меняя их позицию по высоте. У агента есть параметр max slope, с помощью которого мы рассчитываем проходимость ноды, если высота отличается больше, чем на этот угол.

Результат

Для каждого юнита мы находим ноду, на которой он стоит и двигаем его по направлению, которое записано в этой ноде. Тут мы можем добавить steering, т.к. нас в принципе мало интересует где находится юнит в данный момент. Толкают его в сторону - он все равно знает направление, по которому ему нужно следовать.

Дополнительно я записываю в кеш данные по flow field от портала к порталу, чтобы при построении нового пути можно было их переиспользовать.

У нас появилась задача, чтобы сделать библиотеку в игре. Ну чтобы можно было игроку найти нужную информацию о каких-то моментах прямо в игре, а не делать для этого отдельный сайт.

Самый прямой путь к "успеху" был бы использовать uGUI (собственно как у нас и сделана вся верстка в игре). Самый кривой путь - использовать UI Toolkit (пока это не продакшен-реди решение).

Но для первого варианта нужно было бы писать код постоянно (т.е. захотим добавить или переверстать страницу - придется привлекать программиста, художника, верстальщика и прочих людей).

Поэтому я предложил вариант сделать автоматическую верстку из html. Т.е. на вход нам дают html-верстку + css, а дальше оно само верстается (некий аналог UI Toolkit, но с обрезанной функциональностью и с возможностью добавлять любые свои теги, которые бы рисовали префабы вместо себя).

Что мне понадобилось:

https://html-agility-pack.net (парсер для DOM)

https://github.com/TylerBrinks/ExCSS/tree/master (парсер для CSS)

https://github.com/hcesar/HtmlAgilityPack.CssSelector (css-селекторы для DOM)

Дальше все оказалось довольно просто.

Мы заводим массив структур

public struct Node {
     public string tag;
     public string @class;
     public GameObject source;
}

По этому массиву мы будем проходить для каждой ноды и искать нужный префаб, который соответствует конкретному объекту dom (сначала мы ищем по принадлежности класса и тега, а потом уже по тегу).

В итоге получилось что-то такое:

Код (который написан почти в одном файле в стиле "я у мамы программист"):

HTML.zip

• В .net существует 3 поколения: 0, 1 и 2.
• Поколение - это некое хранилище, которое содержит в себе объекты.
• При сборке поколения 0, выжившие объекты переходят в поколение 1.
• В поколении 2 хранятся долгоживущие объекты. Однако, если мысоздаем крупный объект, то он сразу попадает в поколение 2.
• Иногда покление крупных объектов называют поколением 3, но фактически сборка происходит при сборке поколения 2.
• Если размер объекта больше или равен 85 000 байтов, он считается крупным объектом.
• Когда мы собираем старшее поколение, младшие поколения также собираются.
• Объекты, пережившие сборку мусора последнего поколения, по-прежнему будут относиться к этому поколению.
• Если объект меньше 85 000 байтов, он будет помещен в сегмент SOH (куча малых объектов). В противном случае он помещается в сегмент LOH (куча больших объектов).
• SOH сжимается и дефрагментируется, чтобы данные хранились с минимальным оверхедом по памяти.
• LOH по-умолчанию не сжимается, что может приводить к большому потреблению reserved памяти. То есть если большой объект будет удален между существующими объектами, то место не будет освобождено и может быть занято в дальнейшем.
• Для LOH существует возможность сжатия через свойство GCSettings.LargeObjectHeapCompactionMode, таким образом при сборке LOH будет сжиматься и куча больших объектов.

Начнем с того, что это регистры. По сути отличие между ними в том, что xmm (128 bits) хранит меньше данных, чем ymm (256 bits).

Вы можете встретить такое в burst-generated коде, когда разглядываете бесконечные регистры в инспекторе берста.

Пример:

struct MyStruct { 
     public float a1; 
     public float a2; 
     public float a3; 
     public float a4; 
}

myStruct1 = myStruct2 будет использовать xmm (4 флота в 128 битах).

Если же добавить полей:

struct MyStruct { 
     public float a1; 
     public float a2; 
     public float a3; 
     public float a4; 
     public float a5; 
     public float a6; 
     public float a7; 
     public float a8; 
}

то теперь myStruct1 = myStruct2 будет использовать ymm (8 флотов в 256 битах).

Таким образом, мы считаем за одну операцию больше данных.

Но если же мы оставим 6 полей, то будет использован один vmovups xmm, а остальные два поля будут считываться mov rdx.

Есть поле userData, в которое я обычно записываю json, чтобы можно было хранить вменяемую структуру.

Для этого можно использовать AssetImporter::userData.

Есть такая штука, которая позволяет вызывать метод, когда мы не знаем сколько параметров хотим туда передать:

void Method(params object[] arr)

Но есть некоторые особенности, которые нужно понимать:

1. По-умолчанию такой вызов создает новый массив (т.е. триггерит GC, что плохо):

void Method1(params object[] arr)
void Method2(object[] arr)

var arr = new int[10];
Method1(arr); // будет создан массив object[1] и к первому элементу присвоен массив arr
Method2(arr); // будет ошибка компиляции, т.к. object[] не соотвествует типу int[]

2. Если мы передадим точный тип массива, то это не будет создавать новый массив:

void Method1(params int[] arr)
void Method2(int[] arr)

var arr = new int[10];
Method1(arr);
Method2(arr);
// Эти 2 вызова идентичны

3. Любой вызов будет создавать новый массив:

void Method(params int[] arr)

Method(1, 2, 3)
Method(1)

Вывод: избегайте методов с params, особенно если это хот часть.

Совсем недавно ко мне обратился коллега с просьбой помочь с ошибкой, когда json не мог распаковаться и падал с ошибкой примерно такой по смыслу:

"Не могу найти конструктор с передаваемыми параметрами", а стек показывает, что где-то там через рефлексию создается инстанс (через Activator) и при вызове конструктора чет все падает.

И тут знаете, как в шуточках за 300, люди делятся на несколько групп:

• Неопытные с ужасом идут гуглить ошибку, ничего не находят, идут дергать вторую группу;
• Более опытные понимают, что тут как-то не очень все тривиально, идут в место где рефлексией создается какой-то объект и пытаются понять как же можно было накосячить создателям плагина, что оно не работает;
• Ну и такие как мы с вами, которые в принципе уже понимают, что билд скорее всего il2cpp, что рефлексия - это плохо, что il2cpp ничего об этом знать не знает, а значит проблема просто в том, что метода нет после компиляции.

К чему я это все. Для исправления подобных ситуаций, il2cpp нужно "подсказать", что существует метод (или конструктор), для чего я обычно делаю в проекте файл AOT.cs:

public static class AOT {
    [Preserve]
    public static void Dummy() {
       new SomeClass().Method(); // не вырезаем конструктор и метод из билда
       ...
    } 
} 

Т.е. мы никогда не вызываем этот метод, но при сборке эти методы будут добавлены.

Вообще это касается всех вызовов через reflection и когда в проекте не указывается вызов.

Вы, наверное, слышали и встречали такую штуку, а некоторые даже писали.

instance.Method1().Method2()

По своему определению текучие интерфейсы представляют из себя набор методов, где каждый метод добавляет или удаляет какое-то свойство, то есть меняет инстанс.

В принципе я с этим не совсем согласен. Я считаю, что такие методы должны ставить флаги (или просто записывать входные параметры), то есть не должны выполнять работу прямо в месте вызова.

Как? Ну это довольно просто:

void Method() {}

Меняем на

T Method() { return this; }

Где T может быть текущим типом, может быть интерфейсом (как в оригинале было и задумано, но структуры все портят).

Зачем? Лаконичность кода и легкость восприятия.

Пишите в комментах где вы используете fluent-interface подход.

Вообще я уже писал немного про это раньше, но решил расписать более подробно про каждый сэмплер, чтобы было понятно где искать проблему.

WaitForTargetFPS: Время, потраченное на ожидание целевого значения FPS, указанного в Application.targetFrameRate. Редактор не использует VSync на GPU, а вместо этого использует WaitForTargetFPS для имитации задержки VSync.

Gfx.ProcessCommands: Поток рендеринга охватывает всю обработку команд рендеринга. Часть этого времени может быть потрачена на ожидание VSync или новых команд из основного потока, что можно увидеть в Gfx.WaitForPresent.

Gfx.WaitForCommands: Поток рендеринга готов к новым командам, и может указывать на узкое место в основном потоке.

Gfx.PresentFrame: Поток рендеринга представляет собой время, затраченное на ожидание рендеринга и представления кадра графическим процессором, что может включать ожидание VSync.

Gfx.WaitForPresent: Когда основной поток готов начать рендеринг следующего кадра, но поток рендеринга еще не завершил ожидание представления кадра GPU. Это может указывать на то, что узкое место в GPU. Посмотрите на представление временной шкалы, чтобы узнать, проводит ли поток рендеринга одновременно время в Gfx.PresentFrame. Если поток рендеринга все еще проводит время в Camera.Render, узкое место в CPU, т.е. тратит слишком много времени на отправку вызовов отрисовки/текстур на GPU.

С помощью такой простой штуки можно определить насколько совпадают структуры между собой.

На практике такое я применяю для определения равны ли структуры (функция вернет 0) или же отличаются (функция вернет значение больше или меньше нуля, что покажет какая из структур "меньше").

Используйте вместо new T[0]; статичный массив, который не нужно создавать каждый раз.